		*Últimos Cambios*
	Blog personal: El hilo del laberinto

Precisión del sistema GPS

Última Actualización: 18 de febrero de 2005 - Viernes

ATENCIÓN: Las medidas de error expuestas en esta página web se corresponden para una latitud de 40 grados y medio norte, la latitud de Madrid (España). Cada latitud tiene su propia figura de error. En general, el error aumenta a medida que aumenta la latitud. Es decir, a medida que nos movemos hacia los polos.

A continuación muestro los resultados de una prueba de precisión realizada con mi receptor GPS (BT77), durante un período continuo de unas 16 horas.

Lo primero que hay que decir es que el sistema GPS está diseñado para proporcionar una precisión "razonable" para la posición horizontal (latitud y longitud), pero su precisión vertical (altura) es bastante mala.

Para las pruebas, dejé la antena GPS sobre el alfeizar de mi ventana de la oficina, en Madrid (España), tomando lecturas de posición cada segundo, durante 16 horas. En total se tomaron 57076 muestras, que forman la base de este artículo.

En primer lugar vamos a analizar el peor dato, la altura. La coordenada X son segundos, y la Y son metros:

El valor medio es 703.40 metros (la altura real sería de 649.40 metros, ajustando los 54 metros de desviación del geoide en mi localización). Pero la medida mínima es 649.8 metros y la máxima 793.6. Es decir, llegamos a tener errores de altura de hasta 90 metros, que se dice pronto :-(. Peor aún, dado que las medidas tienen una correlación importante, no podemos reducir el error simplemente promediando medidas sucesivas. Si estamos utilizando el GPS para obtener un perfil de alturas en una ruta, el resultado será desastroso, a menos que apliquemos correcciones DGPS o similares.

¿Cuál es el error esperable en una medida al azar?. La tabla es aproximadamente la siguiente:

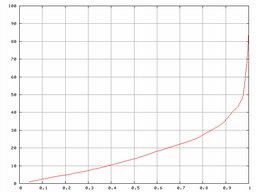
El eje X es la probabilidad, y el Y los metros de error. Es decir, que el 40% de las medidas "aleatorias" tendrán un error inferior a los 10 metros. El 95% de las medidas tienen un error inferior a los 45 metros. Sólo el 4% de las medidas tienen un error inferior al metro.

La gráfica nos da el error estimado en el caso de medidas aisladas. No se puede aplicar en el caso de tomar varias medidas, porque no estamos valorando la correlación que existe entre medidas próximas en el tiempo.

La situación es parecida en el caso de la posición horizontal (latitud y longitud), aunque en este caso los valores obtenidos son bastante más precisos, y su trazado en un mapa de ruta es mucho menos delicado que la altura. Los gráficos correspondientes son, para las coordenadas de Madrid (España):

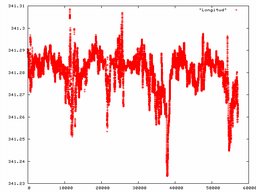
En estos gráficos, el eje X es el tiempo en segundos, y el eje Y es grados*100+minutos de arco. Volvemos a ver una gran correlacion entre medidas cercanas en el tiempo, por lo que no solucionamos nada promediando medidas sucesivas.

Podemos trazar directamente el mapa de latitud y longitud:

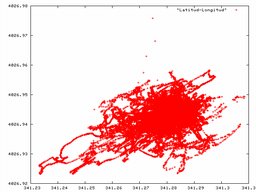
En buena lógica la nube de puntos debería ser más o menos circular, pero parece no ser el caso. Pero ello es debido a que la tierra es una esfera (por mucho que los mapas sean "planos" :-). En realidad, para la latitud de Madrid (España), cada minuto de arco de latitud supone una milla náutica (1852 metros), pero cada minuto de longitud mide solo 1412.46 metros. Si ajustamos la misma escala en ambos ejes, que es como saldría en un mapa, tenemos:

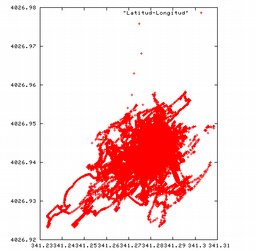
Pero lo que nos interesa es el error. Calculando la media de estas 16 horas, nos sale que nuestra posición es 40 grados y 26.943 minutos norte, y 3 grados y 41.280 minutos oeste. Calculando el error de posición horizontal, tenemos esta evolución a lo largo del tiempo:

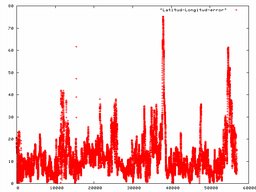
El eje horizontal son segundos, y el vertical metros. Vemos, como siempre, correlación entre medidas sucesivas. En este caso, no obstante, los errores de posición horizontal son bastante inferiores a los errores de altitud. El error máximo medido durante la recogida de datos fue de 75 metros.

Calculando el error esperable en una medida al azar, como antes, tenemos:

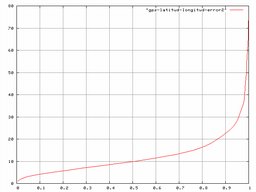
El eje X es la probabilidad, y el Y los metros de error. Es decir, que el 50% de las medidas "aleatorias" tendrán un error inferior a los 10 metros. El 86% de las medidas tienen un error inferior a los 20 metros. El 95% de las medidas tiene un error inferior a 30 metros.

Algunas conclusiones:

Aunque los errores de altitud no tienen una magnitud muy superior a los de posición horizontal, son menos tolerables en mapas de rutas.
Aunque la probabilidad de que una medida sea muy mala es baja, dado que existe una gran correlación entre medidas adyacentes, es muy posible que las medidas realizadas en el mismo entorno temporal estén también muy desviadas.
Los errores entre las tres magnitudes medidas (latitud, longitud y altitud) guardan una cierta correlación (se ven picos de error en los mismos lugares temporales). Muy posiblemente se deban a posicionamientos poco satisfactorios de la constelación de satélites GPS. No parece deberse a problemas de ocultación por algún edificio, porque en los momentos con mayor error se toman medidas de hasta 8 satélites distintos, simultaneamente.
En este estudio no estoy considerando información PDOP (Positional Dilution Of Precision), VDOP y HDOP.

Te puedes descargar las mediciones en bruto (1'5Mbytes, formato GZIP; se expande a 23MB), en formato NMEA.

Más información sobre los OpenBadges

Donación BitCoin: 19niBN42ac2pqDQFx6GJZxry2JQSFvwAfS